Boyle’s Law of Ideal Gasses Study Guide
Lesson Objectives
- Define Boyle’s law
- Describe the relationship between the pressure, P, of a gas and the volume, V, of its container at a constant amount of gas and temperature
- Determine the pressure or volume of a gas before or after a chemical or thermodynamic process using the equation
- Derive the Boyle’s law equation
Introduction
We all know that getting a shot at the doctor’s office isn’t exactly a fun experience (except for at the end when you get candy and a cool band-aid). What you might not know is that the process of giving a shot is an everyday example of Boyle’s law, which states that the pressure of a gas is inversely proportional to the volume of space it occupies when temperature and the number of gas particles are held constant.
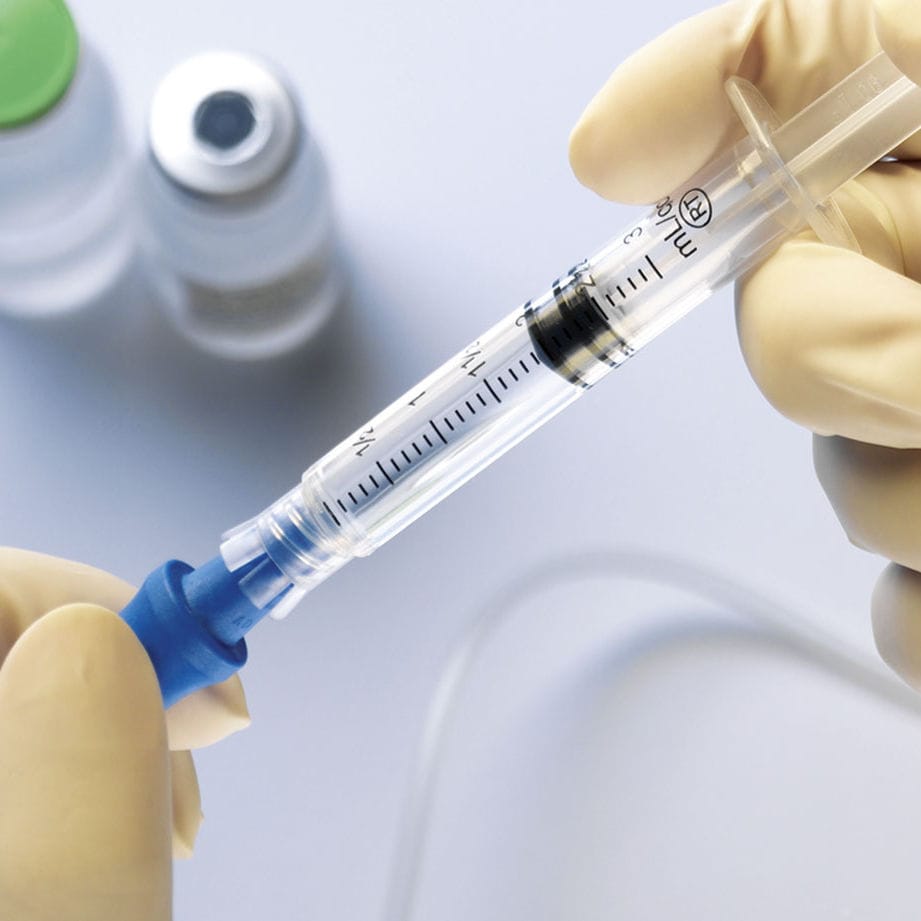
Because the syringe is capped, the amount of gas inside remains constant, as does the temperature of the air surrounding it. When the doctor pulls back the plunger, the volume of the syringe increases, and the pressure decreases. This change in pressure causes the medication to enter the cavity. When the doctor pushes the plunger in to give the shot, the opposite process occurs, as the volume of the syringe decreases while the pressure increases, pushing the medicine out again.
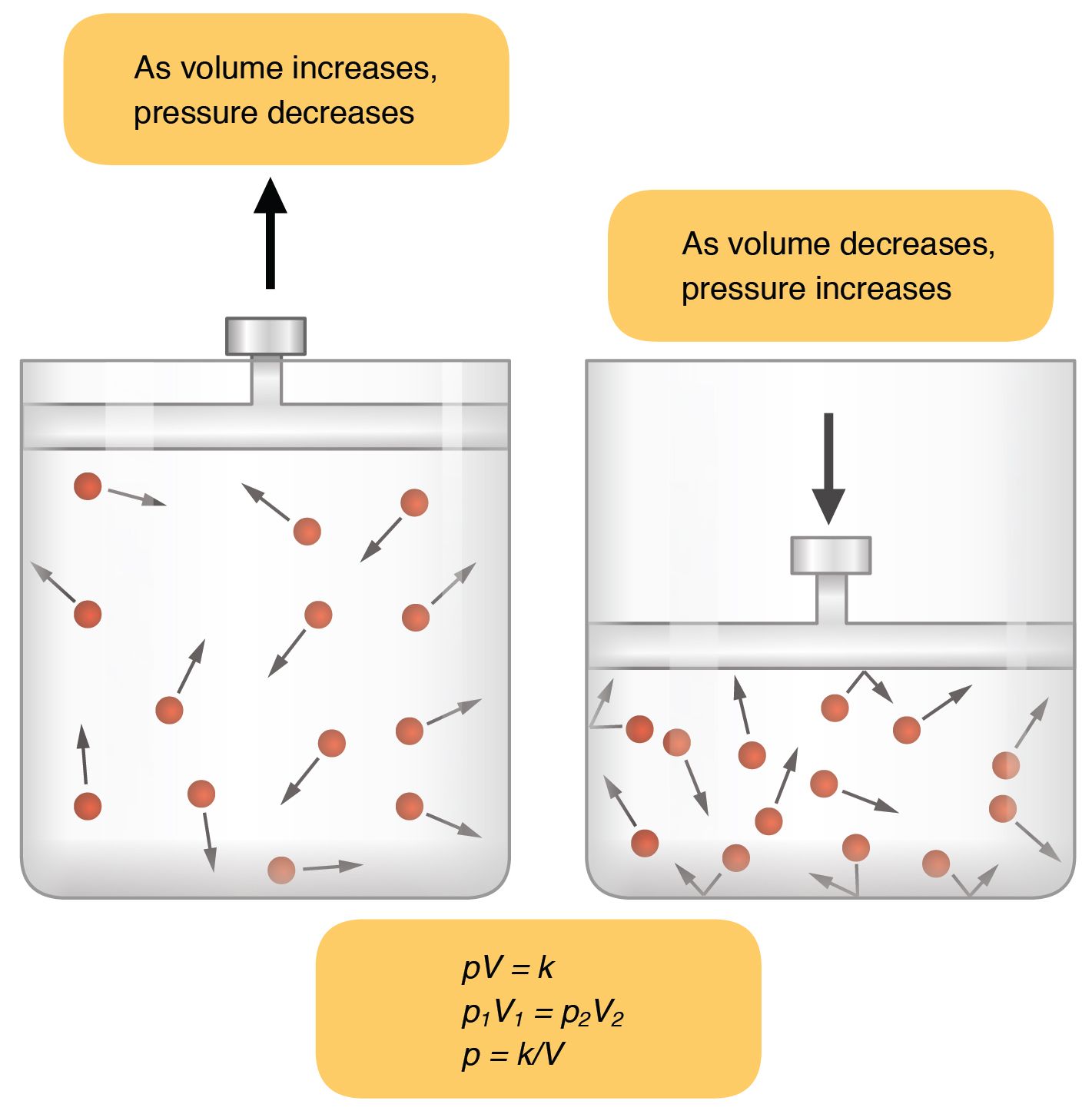
Boyle’s Law
As mentioned before, Boyle’s law states the pressure of the gas is inversely proportional to the volume of space it occupies when temperature and the number of gas particles are held constant. Let’s try to visualize this by imagining a container filled with gas.
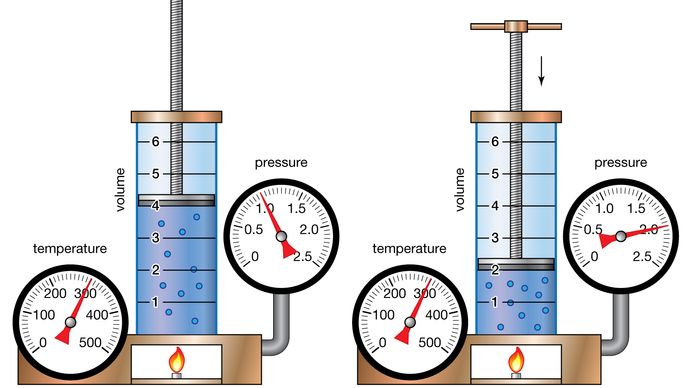
Gas particles have high kinetic energy and move rapidly in all directions, frequently colliding with one another and bouncing off the walls of the vessel that contains them. As a result, gasses have no defined shape and expand to occupy the entire volume of their container. So what happens if you reduce the size of the container while keeping the temperature and number of gas particles inside the same?
Because gas expands to occupy the entire volume of its container, a decrease in vessel size will result in a decrease in volume. The same amount of gas in a smaller space increases the number of collisions between the particles and the walls of the vessel. As per Boyle’s law, the pressure exerted by the gas is inversely proportional to its volume; thus, with a decrease in volume, gas pressure increases. Let’s dive deeper into the nuances of Boyle’s law starting with the derivation of the Boyle’s law formula.
Boyle’s Law Formula & Derivation
We know that under ideal conditions, pressure is inversely proportional to the volume of gas. The mathematical expression of Boyle’s law can be written as:
P ∝ (1 ÷ V)
Where:
- P is pressure
- V is volume
To translate this equation into an algebraic form, we will have to replace the inverse sign ∝ with a constant. For this we use Boyle’s constant, k, which can be determined using the following formula:
k = PV
Where:
- k = Boyle’s constant
- P = pressure
- V = volume
This equation can be derived from either:
V = k ÷ P or P = k ÷ V
The inverse nature of this relationship tells us that when pressure or volume change, the product of the initial pressure and volume will be equal to the product of the final pressure and volume. Thus, Boyle’s law equation is written as:
P₁V₁ = P₂V₂
Where:
- P₁ is initial pressure
- V₁ is initial volume
- P₂ is final pressure
- V₂ is final volume.
This equation is derived from the formula for Boyle’s constant, the process of which can be seen below.
P₁V₁ = kP₂V₂ = k
P₁V₁ = P₂V₂
💡 Summary
-
Boyle’s gas law states the pressure of the gas is inversely proportional to the volume of space it occupies when temperature and the number of gas particles are held constant.
-
The basic formula for gas pressure according to this law is P ∝ (1 ÷ V).
-
To translate this equation into algebraic terms, we need to replace the inverse sign ∝ with a constant. The formula for Boyle’s constant is k = P V.
-
We can use the Boyle’s constant formula to find the new pressure of a gas following a change in volume by combining the initial value of Boyle’s constant k = P1V1 with the final value k = P₂V₂.
-
The result is the algebraic version of the Boyle’s law formula, P₁V₁ = P₂V₂.
🧐 FAQs
1. What is Boyle’s law?
Boyle’s law states that when temperature and the quantity of gas are held constant, the pressure exerted by the gas is inversely proportional to the volume occupied.
2. What is the formula used to represent Boyle’s law?
The mathematical expression for Boyle’s law formula is: P₁V₁ = P₂V₂.
We hope you enjoyed studying this lesson and learned something cool about Boyle’s Law Of Ideal Gases! Join our Discord community to get any questions you may have answered and to engage with other students just like you! Don’t forget to download our App to experience our fun, VR classrooms – we promise, it makes studying much more fun! 😎
Sources
- Boyle’s Law: https://chem.libretexts.org/Bookshelves/Introductory_Chemistry/Introductory_Chemistry_(CK-12)/14%3A_The_Behavior_of_Gases/14.03%3A_Boyle’s_Law.Accessed 9th March 2022.
- Boyle’s Law of Ideal Gases: https://www.ck12.org/c/chemistry/boyles-law/lecture/The-Sci-Guys%253A-Boyles-Law-of-Ideal-Gases/.Accessed 9th March 2022.
