In the present-day formula one race weekend, one car can reach speeds of up to 200 miles per hour, but when the five red lights come off, all the awaiting drivers are morally and physically equal. The initial velocity of the drivers is zero before they press the gas pedal. We could indeed say that the velocity of these cars changes over time at different points. As they approach the checkered flag, the best of these drivers reach their top velocity.

Instantaneous Velocity

• The instantaneous velocity of an object, sometimes known as just velocity, is a statistic that tells us how quickly an object is going somewhere along its route.
• It’s the average velocity between two places on a path in the limit when the time (and thus the displacement) between them reaches zero.
• Clearly, the definition of instantaneous velocity can be the rate at which a person’s position changes over a short period of time (almost zero).
• The SI unit of instantaneous velocity is m/s. The magnitude of the instantaneous velocity is known as instantaneous speed.
• Its value is identical to that of instantaneous velocity, but it has no direction.

Instantaneous Velocity Formula

The formula of the instantaneous velocity is expressed mathematically by using the formula for the average velocity.

Average velocity (V) = x(t2) – x(t1) ( net displacement ) / t2 – t1 ( net time)

In order to find the instantaneous velocity at an arbitrary position, we assume t1= t and t2= t+Δ t. After using these values in the formula of the average velocity, we take the limit as
Δt →0 and find the expression of the instantaneous velocity

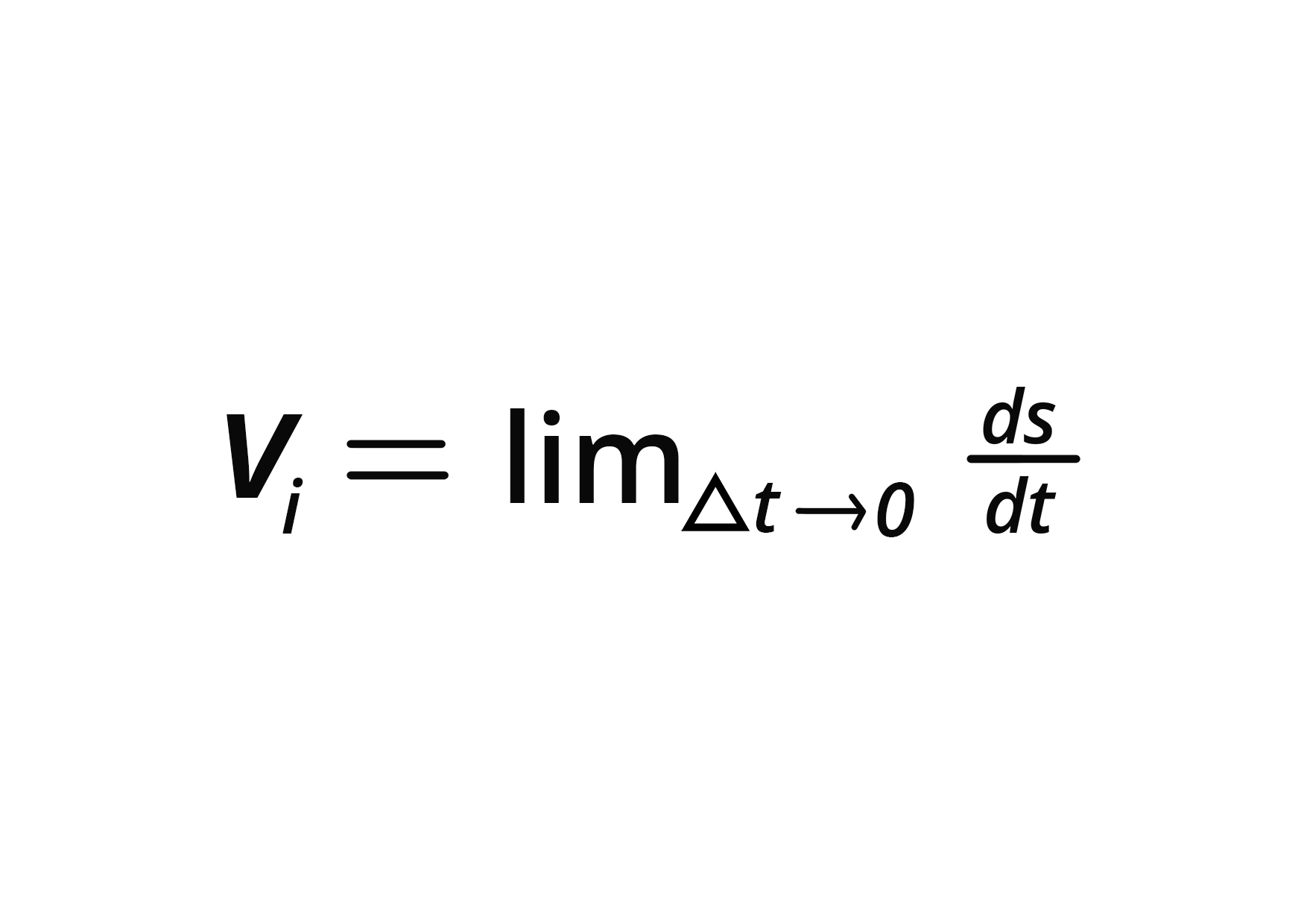
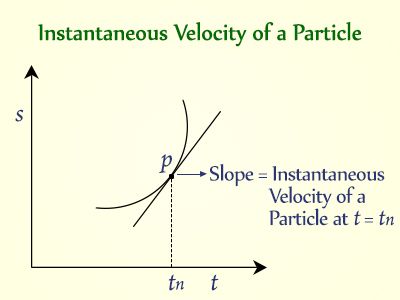
The slope of the distance-time graph, often known as the x-t graph, can also be used to determine it.

Instantaneous Velocity Example

An example of the instantaneous velocity can be:

If the object’s displacement changes with time and therefore is given as (5t2+3t+4) m, the instantaneous velocity can be calculated at any time by:

s= (5t2+3t+4)Velocity (v) = 10t+3

So, if we need to calculate the instantaneous velocity at t = 10 seconds, we’ll plug the constant into the velocity expression.

Therefore the instantaneous velocity at t=10 s will be 103 m/s The displacement, in this case, will be 534 meters ( using the values of t in the given expression )

And the average velocity will be 534/10= 53.4 m/s.

AVERAGE VS INSTANTANEOUS VELOCITY

• It’s worth noting in the above example that the object had different average and instantaneous velocities.
• The instantaneous velocity is the rate of change of position (or displacement) with respect to the time at a fixed place, whereas the average velocity is the rate of change of position over a period of time.
• It’s only when the body will move at a constant velocity, that the instantaneous velocity and the average velocity would be equal.

SUMMARY

• The instantaneous velocity is the velocity of a moving item at a certain moment in time.
• Instantaneous velocity is a vector quantity.
• v ( instantaneous) = limitΔt →0 ds/dt, where ds is net displacement, and dt is the net time.

FAQs

1. Write the expression for instantaneous velocity.

The mathematical expression for the instantaneous velocity will be v ( instantaneous) = limit Δt →0 ds/dt, where ds is net displacement, and dt is the net time.

2. What do you understand about instantaneous velocity?

The instantaneous velocity can be easily understood as the velocity of a moving item at a certain moment in time.

3. How to calculate instantaneous velocity?

The instantaneous velocity can be calculated using v ( instantaneous) = limit Δt →0 ds/dt, where ds is net displacement and dt is the net time.

4. When will the average velocity be equal to instantaneous velocity?

In a motion where an object moves with constant velocity, the average and the instantaneous velocity will be equal.

We hope you enjoyed studying this lesson and learned something cool about Instantaneous Velocity! Join our Discord community to get any questions you may have answered and to engage with other students just like you! We promise, it makes studying much more fun!😎

]]>