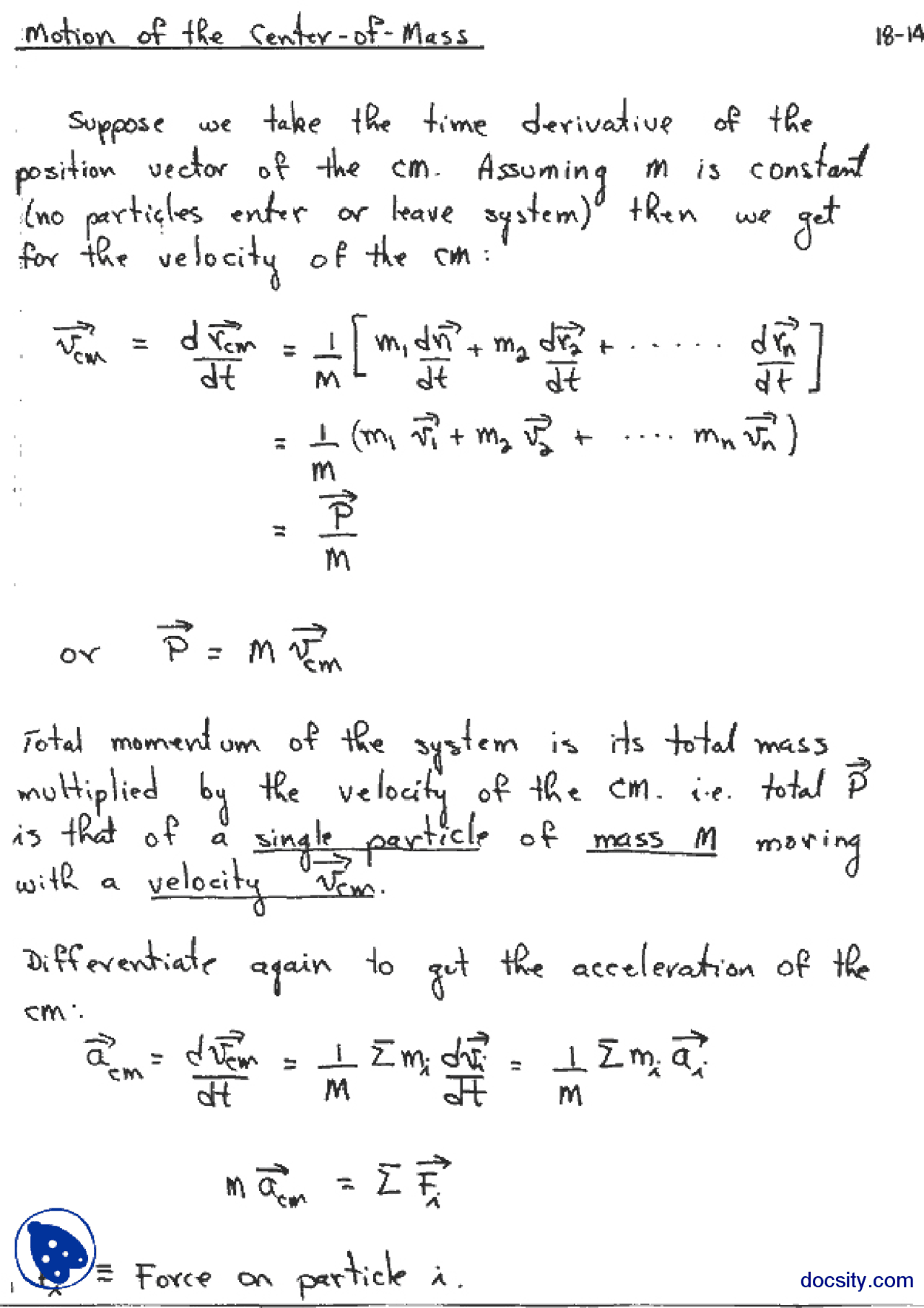CBSE Class 11 Physics Chapter 7 Revision Notes

Chapter 7: Systems of Particles and Rotational Motion Revision Notes

• A rigid body is one whose shape is perfectly defined and unchanging. The distances between all pairs of particles in a body like this remain constant.
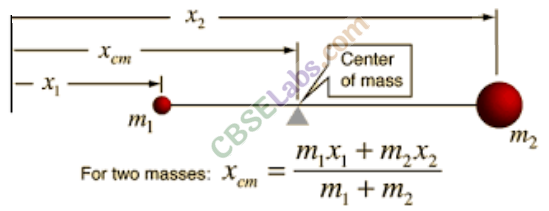
• Mass Concentration: For the purposes of considering the translational motion of a system of particles, the center of mass is defined as the point where the entire mass of the system is imagined to be concentrated.
• If all external forces acting on the body/system of bodies were applied at the center of mass, the body/system of bodies’ state of rest/motion would be unaffected.
• The balancing point of a body or system is its center of mass.
• The center of mass of a two-particle system is always on the line that connects the two particles and is located in the middle.

Source

• Motion of center of mass: The center of mass of a system of particles moves as if all of the system’s mass were concentrated at that point and all external forces were applied there. The velocity of a system of two particles, m1 and m2, with velocities v1 and v2, is given by,

Source

• If there is no external force acting on the body, the center of mass will maintain its momentum. It has a constant velocity and no acceleration, so MV_cm = constant.

Torque

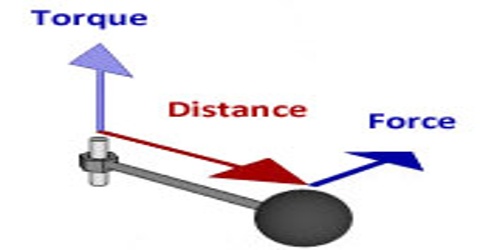
• The moment of force is defined as torque.
• The product of the magnitude of the force acting on the particle and the perpendicular distance of the force application from the particle’s axis of rotation is the torque acting on the particle.

Source

• Angular Momentum: The magnitude of angular momentum (or moment of momentum) around an axis of rotation is equal to the product of momentum and the perpendicular distance of the line of action of momentum from the axis of rotation, and its direction is perpendicular to the plane containing the momentum and the perpendicular distance.

• Axis of Rotation: If each point mass that makes up a rigid body describes a circular path with a different radius but the same angular speed, it is said to be rotating. All of the point masses’ circular paths have a common center. The axis of rotation is a line that passes through this common center. If a rigid body remains in its rest or uniform motion under the action of forces/torques, it is said to be in equilibrium.

• The vector sum of all forces acting on a body must be zero for translational equilibrium. The vector sum of torques of all forces acting on that body around the reference point must be zero for rotational equilibrium. Both of these conditions must be met for complete equilibrium.

• Couple is made up of two equal and opposing forces acting on the same body but on opposing lines of action. A couple’s net force is zero, but they produce rotational motion by exerting torque.

• Moment of inertia: The moment of inertia of a rigid body refers to its rotational inertia.

The sum of the products of the masses of the particles that make up the body and the square of their respective perpendicular distance from the axis is the moment of inertia of the body around an axis.

Radius of Gyration:

• The radius of gyration is the distance between a point in a body and the axis of rotation at which, if the entire mass of the body were concentrated, its moment of inertia about the axis of rotation would be the same as that determined by the actual distribution of mass of the body.
• If the body’s entire mass is concentrated at a distance K from the axis of rotation, the moment of inertia I can be written as I = MK2.

]]>