Circuit Construction Study Guide
INTRODUCTION
In your Physics class, you have studied simple series and parallel circuits. A bulb connected to a battery is the simplest circuit to determine the source of voltage and resistance. Add the second bulb in series, and now you have another source of resistance.
An equivalent circuit for this loop can be modeled easily by lumping the components. The same applies to simple parallel circuits.
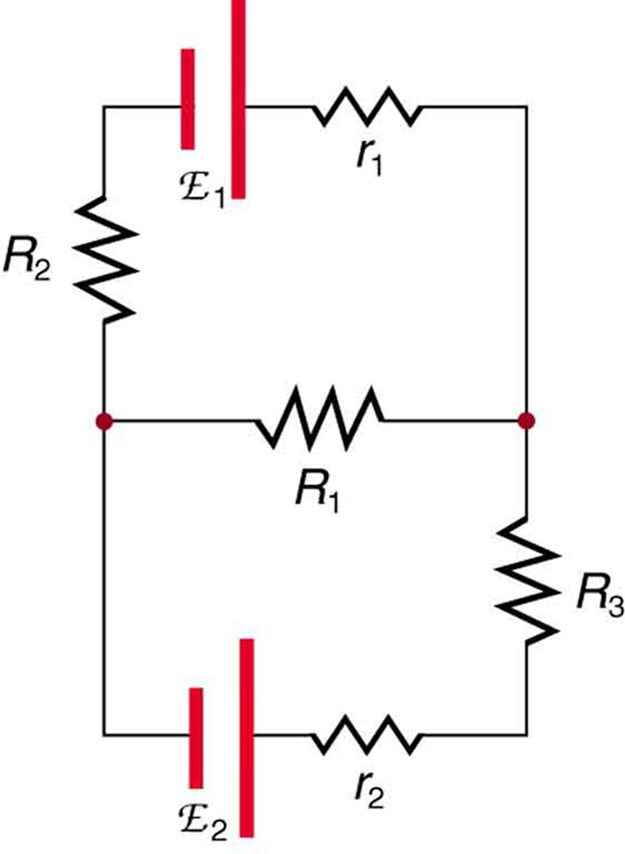
What happens when there is a multi-loop circuit with junctions like in the diagram below? How would you analyze the current flow and voltage drops? Enter the kirchhoffs law!
WHAT IS KIRCHHOFF’S LAW?
These laws named after Gustav Kirchhoff (1824-1887) show us how to analyze complicated closed circuits. It has two basic rules that are related to voltage and current in electrical circuits:
KIRCHHOFF’S FIRST RULE
Also known as Kirchhoff’s Junction law, the rule applies to electrical charges entering and leaving a junction. A junction in an electrical circuit is a point where three or more circuit elements meet and the current splits.
Consider the diagram below:
An electric current is the flow of charge, and at any given point the charge is conserved. So, the current that flows into the junction is the current that flows out.
Therefore we have the first rule: The sum of all currents entering the junction must be equal to the sum of all currents leaving the junction.
Mathematically, it is expressed as: ΣIin = ΣIout
To better visualize it, think of the above diagram like a junction of water pipes. The amount of water flowing is the current. The total water entering the junction is the same as the total water leaving the junction.
2. KIRCHHOFF’S SECOND RULE
Also known as the kirchhoff’s Loop rule, the rule relates to the voltage in a closed circuit.
It states that: The algebraic sum of voltage drop around a closed circuit path is zero.
Mathematically that is: ΣV= 0
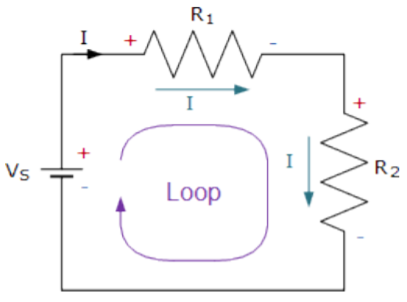
Consider the circuit above. There’s a source of potential or voltage (Vs) and two components with resistance R1 and R2. In a series loop, the voltage drops across the components as the potential gets used up by the devices. Therefore, according to Kirchhoff’s law, the algebraic sum of all voltages, including the source and the resistive elements, is equal to zero.
Mathematically it is expressed as:
Vs = IR1+IR2Or Vs – IR1 – IR2 = 0
CONCLUSION:
- Kirchhoff’s laws can be used to analyze complex multi-loop circuits.
- Kirchhoff’s Junction law states that the sum of all currents entering the junction must be equal to the sum of all currents leaving the junction.
- Kirchhoff’s Loop rule states that The algebraic sum of voltage drop around a closed circuit path is zero.
FAQs:
1. How do you do circuit construction?
Part of circuit construction is to analyze the circuits using Kirchhoff’s current and voltage laws. The currents and voltages across components can be calculated before building the actual circuit.
2. How do you construct a series circuit in a circuit?
In a series circuit, the leads are connected in a circular loop. A circuit with a bulb and a motor powered by a battery can be connected by joining one end of each motor and bulb together. The two other ends are connected to the battery to complete the series circuit.
We hope you enjoyed studying this lesson and learned something cool about Circuit Construction! Join our Discord community to get any questions you may have answered and to engage with other students just like you! We promise, it makes studying much more fun! 😎
SOURCES:
- 20.11 Circuit. https://flexbooks.ck12.org/cbook/ck-12-middle-school-physical-science-flexbook-2.0/section/20.11/primary/lesson/electric-circuits-ms-ps/. Accessed 10 Feb 2022.
- Circuit Diagrams – Overview. https://www.ck12.org/c/physics/circuits/enrichment/Circuit-Diagrams-Overview/?referrer=concept_details. Accessed 10 Feb 2022.
- Kirchhoff’s Law. https://byjus.com/physics/kirchhoffs-law/. Accessed 10 Feb 2022.
- Kirchhoff’s Rules. https://courses.lumenlearning.com/physics/chapter/21-3-kirchhoffs-rules/. Accessed 10 Feb 2022.
- Kirchhoff’s Voltage Law. https://www.electronics-tutorials.ws/dccircuits/kirchhoffs-voltage-law.html. Accessed 10 Feb 2022.