What is Average Velocity?

We generally hear that now everyone wishes to pitch a baseball as fast as they can. In fact, we all idealise the famous rookie Aroldis Chapman for his 105.1 miles per hour fireball. But the term ‘fast’ here is a vague term for the physical concept of velocity. The maximum speed of a specific pitch at any moment from its release to the time it crosses home plate is represented as velocity, one of the most commonly utilized tools for evaluating pitchers.

Finding Average Velocity

Finding average velocity is similar to finding average speed, and it's the rate at which an object moves over time.

VELOCITY AND SPEED

The terms speed and velocity are commonly used interchangeably in everyday language to describe how fast an object is moving. Nevertheless, they are significantly different in physics. The magnitude of an object's velocity, regardless of direction, is called speed. Velocity rather encompasses both speed and direction. Because it's a vector, it needs a magnitude and a direction.

AVERAGE VELOCITY

• Average velocity’s definition is the time duration of the object selected divided by the displacement in relation to the initial position.
• To put it another way, it's the rate at which an object moves over time.
• The SI unit of average velocity is similar to the average speed, in meters per second.
• The average velocity's direction is the displacement's direction.
• Even though the item's speed varies and its magnitude changes, the item's direction remains the same as that of the direction of displacement.
• As displacement is less than or equivalent to the distance traveled, the quantity of average velocity is less than or equivalent to the average speed.

AVERAGE VELOCITY FORMULA

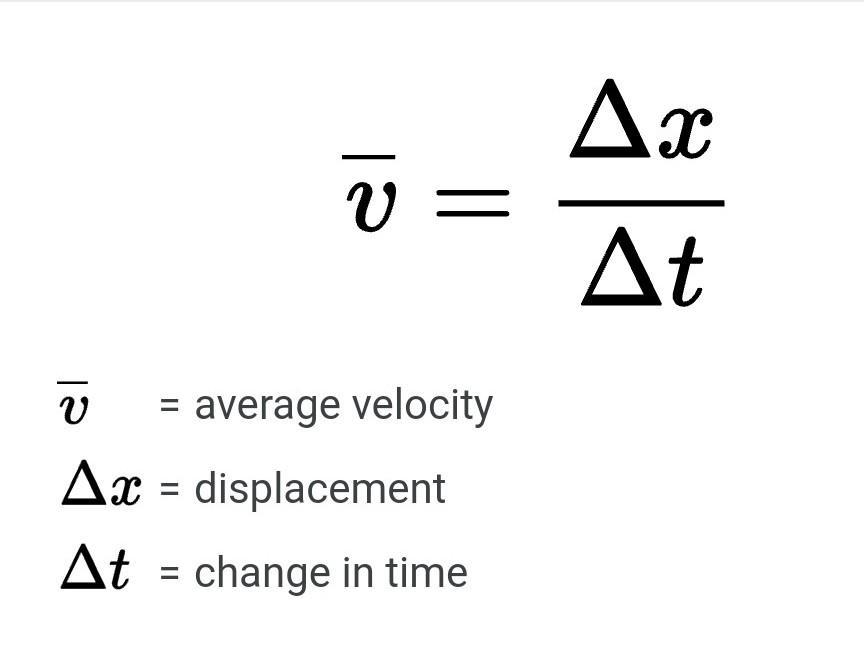
• The formulae for the average velocity and the average speed are the same ( described in the image), but the only variation is the type of physical measure, which is speed or velocity in this case.
• Speed is a single-magnitude scalar quantity.
• Velocity, on the other hand, is a vector quantity with both magnitude and direction.
• The mathematical description of average velocity can be

Average velocity (V) = x1 - x2 ( net displacement ) / t1 - t2 ( net time)

An example of the average velocity can be

Example 1. In 5 hours, a truck driver travels 20 miles ( 32.18 KM) down the road. He then changes direction and travels 12 miles ( 19.3 KM) in 3 hours. What's his average velocity?

We know v ( average velocity ) = net displacement / net time Therefore , v = (20- 12)/ (5 3 ) And finally, the average velocity will be 1 kilometer/hour.

Example 2. A car is moving along the surface OA. It moves from O to A in 18 seconds and returns A to B in 6 seconds. If OA = 360 meter and OB = 240 meter then find average velocity from – O to A and O to B.

OA = OB + AB 360 = 240 – AB AB = 120 meter

Average velocity for O to A = Total displacement / Total time = 360 m (Along OA) / 18 sec = 20 m/s (Along OA)

Average velocity for O to B Average velocity = Total displacement / Total time

O is the initial point and B is the final point. We will consider the shortest distance between O and A which is O and B

Average velocity = OB (Along OB) / Time OA + Time AB = 240 m (Along OB) / 18 sec + 6 sec = 10 m/s (Along OB)

The average velocity (Along O to A) is 20 m/s The average velocity (Along O to B) is 10 m/s

Difference between Average Speed and Average Velocity

The primary distinction between speed and velocity is that speed is a scalar quantity that only considers distance travelled, but velocity is a vector quantity that also considers direction, and velocity depends upon displacement.

Average Speed: It is the total distance travelled divided by the total time taken to cover that distance.

Average Speed = Total distance covered / Total time taken In case of uniform motion the overall speed remains the same. Average speed is used to find out the overall speed in case of non-uniform motion.

Example: An object travels 16m in 4 seconds and then another 16m in 2 seconds. What is the average speed of the object?

Answer: D1 = 16 m T1 = 4s D2 = 16 m T2 = 2s

Total distance = D1 + D2 = 16 + 16 = 32 m Total time taken = T1 + T2 = 2 + 4 = 6 s Average speed = 32m / 6s = 5.33 m/s The average speed of the object is 5.33 m/s

Average Velocity

It is the total displacement divided by the total time taken to cover that distance. Average velocity = Total displacement / Total time

If the velocity is changing but at uniform rate than the average velocity will be arithmetic mean of initial and final velocities. In such a case we will have to use the following formula-

Average Velocity = Initial velocity + Final velocity / 2

Example. Usha swims in a 90 m long pool. She covers 180 m in one minute by swimming from one end to the other and back along the same straight path. Find out the average speed and the average velocity of Usha.

Answer: Total distance covered by Usha in 1 min is 180 m

Displacement of Usha in 1 min = 0 m 1 minute is converted in seconds 1 min = 60 sec Average speed = Total distance covered / Total time taken = 180 m / 60 s = 3 ms-1 Average Velocity = Total Displacement / Total time taken = 0m / 60s = 0ms-1

The average velocity of Usha is 0 ms-1

Magnitude of Average Velocity

Magnitude of average velocity of an object is equal to its average speed only when the object is moving in a straight line.

Question. In 1 second a particle goes from A to B moving in semi-circle of radius 1.0 meter. Find out the magnitude of average velocity.

Answer: Average velocity = Total displacement / Total time Average velocity = 2 m / 1 s = 2 m/s The magnitude of average velocity of the particle is 2 m/s.

Average Angular Velocity

The average pace at which an object rotates over a specific period of time is referred to as its average angular velocity. Angular velocity measures how fast or how slow a body is rotating or it can be even said as how much angular displacement a body covers in one second. It is a vector quantity.

Angular velocity is denoted by Omega (ω).

Formula of Angular Velocity is ω = change in angular displacement / change in time = (Final angular coordinate) – (Initial angular coordinate) / (Final time) – (Initial time)

SUMMARY

• The magnitude of an object's velocity, regardless of direction, is called speed, and Velocity encompasses both speed and direction.
• Average velocity’s definition is the time duration of the object selected divided by the displacement in relation to the initial position.
• The formula for the average velocity and the average speed are same Average velocity (V) = x1 - x2 ( net displacement ) / t1 - t2 ( net time)

FAQs

1. When is the average velocity zero?

The average velocity will be zero in all the cases where the net displacement would be zero.

2. Can average velocity be zero?

Yes, when the net displacement is zero, the average velocity would be zero.

3. Is Average velocity a vector or a scalar?

Just like velocity, the average velocity has a direction and therefore is a vector quantity.

4. How to calculate average velocity?

Average velocity can be calculated using the formula. Average velocity (V) = x1 - x2 ( net displacement ) / t1 - t2 ( net time)

We hope you enjoyed studying this lesson and learned something cool about Average Velocity! Join our Discord community to get any questions you may have answered and to engage with other students just like you! Don't forget to download our App to experience our fun VR classrooms - we promise, it makes studying much more fun!😎