Significant Figures Study Guide

The precision of any number can be communicated by significant figures. Significant figures use different numbers of digits to express the level of precision of a measurement. Use this significant figures crash course to help you learn more about how they work!

WHAT ARE SIGNIFICANT FIGURES

A significant figure is the number of digits in the obtained value after rounding off the decimal values. They are often referred to as a quick measurement that contributes to the accuracy level of the value. Zero is said to be an insignificant figure; significant values begin with the first non-zero digit of a number. The number of significant figures obtained after rounding up is called the precision of the number.

CONVERSION OF SIGNIFICANT FIGURES

The conversion of significant figures is easy with the use of a calculator. To do it manually, there are a few simple rules to follow.

• All non-zero digits are significant figures. The number 22.45 has four significant figures because all of its digits are non-zero.
• Zeros found between non-zero digits are significant figures. The number 2003 has 4 significant figures because the zeros are between the non-zero digits 2 and 3.
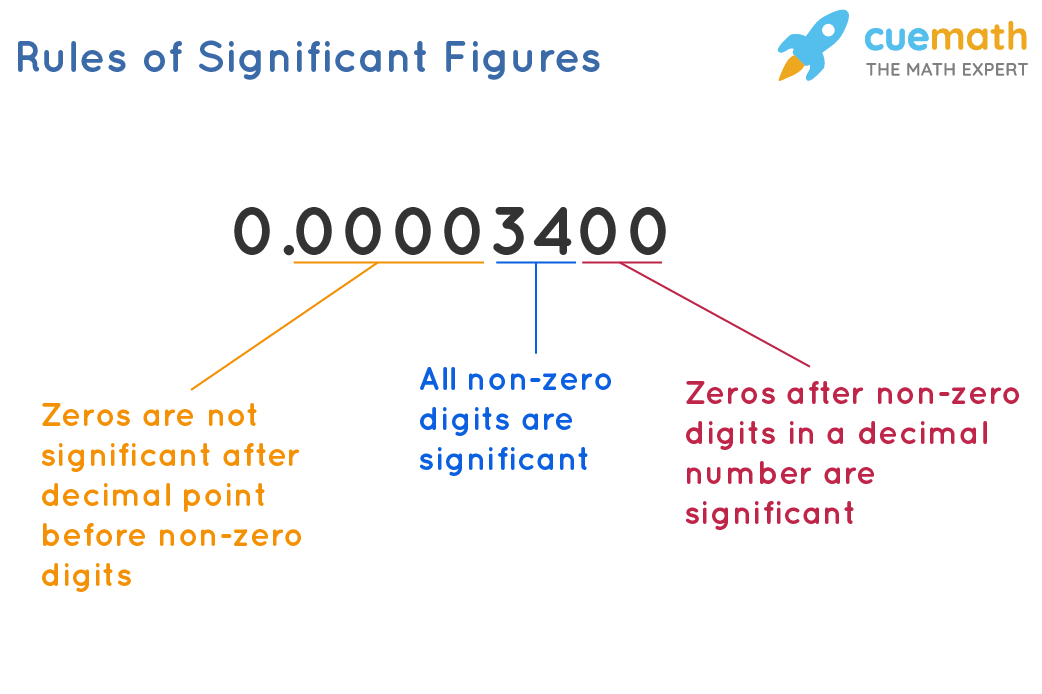
• Leading zeros are not significant figures. The number 0.14 has 2 significant figures, as does 0.014, 0.0014, and so on.
• Trailing zeros are significant figures, but only to the right of the decimal point. There are 4 significant figures in 4.000.
• Trailing zeros in a whole number are significant only if followed by a decimal point. The number 6000 only has one significant figure, but 6000. has 4.
• For a number in scientific notation N x 10x, only the digits comprising N are significant. 3.45 x 102 and 3.45 x 103 both have 3 significant figures.

How to Round a Significant Figure

The technique of rounding to a significant figure is frequently employed since it may be utilised with any kind of number, no matter how large or small. When a newspaper writes that a lottery winner has won $5 million, it has rounded the amount to one large number. The most significant digit in the number is rounded up.

• If you’re rounding to one significant figure, look at the first non-zero digit.
• Examine the digit that follows the first non-zero digit.
• If two significant figures are added after the required place value digit, draw a vertical line to reveal the following digit.
• Increase the previous digit by one if it is 5 or more.
• Keeping the previous digit the same if the number is 4 or less means filling in any blank spaces to the right of the line with zeros and stopping at the decimal point if there is one.

Example

__Question: Round 0.004031 to 3 significant f__igures.

Explanation: The first thing we do is find the third significant figure, which is three, and we can label 1 as our last digit. We look at the number on the right, which is our decider, and because it’s 1, which counts as 4 or less, it tells us we are going to have to keep the last digit the same. So we keep our last digit, 3, and the decider becomes zero. Whenever we round a decimal like this, we actually don’t keep any zeros at the end of the number, so we would get rid of it and end up with 0.00403.

Answer: 0.00403

Question: Round 3476 to 2 Significant Figures

Explanation: Firstly, find the second significant figure, which is 4; we can call it the last digit, and this is the number we have to round up or down. To figure it out, we have to look at the next digit, which is the 7. It will be the decider. If the decider is 5 or more, we have to round up the last digit. So as the decider is 7, we have to round the second number, which is 4, up to 5, and we will have to change the last two digits to 00, giving us 3500 as our answer.

Answer: 3500

CONCLUSION

• The significant figures refer to the part, which includes the single-digit numbers from 0 to 9 as the coefficient in expression.
• Significant figures follow a certain set of rules and accurately work on them.
• In precision, when the measurement level gets repeated, it gives out the identical result, and the individual measured results agree with each other.

FAQs

1. What are the 5 Rules of significant figures?

Five rules are:

• All non-zero digits are significant.
• Between two non-zero digits, if any zero is placed, it is significant.
• Leading zeros are insignificant.
• Trailing zeros without any decimal is insignificant.
• Any number with scientific notation is said to be significant.

2. How do you do significant figures easily?

Significant figures are non-zero digits, which do not count any leading or trailing zeros. To easily do the crash course sig figs, maintain the identical significant figures while going through the decimal and scientific notations. Other ways to do them are by following pacific and Atlantic rules.

3. What are the rules for counting significant figures?

• If the next digit to the number is more than or equal to five, then the number is rounded up, while if it is less than five, the number is rounded down.
• In multiplication and division, maintain the same significant figures.
• In addition or subtraction, maintain the same number of decimal places.

4. How do you teach significant figures?

Significant figures used in unit conversion Chemistry help one teach and understand them. If you want to round up the 489 to the one significant figure, you can easily obtain 500 as the significant value. For example, is 0.00034 a significant figure? We can say that the zeros to the left side are always considered an insignificant value, and thus only 34 is the significant figure in this value.

We hope you enjoyed studying this lesson and learned something cool about the Significant Figures Crash Course! Join our Discord community to get any questions you may have answered and to engage with other students just like you! Don’t forget to download our app to experience our fun VR classrooms – we promise it makes studying much more fun! 😎

]]>