Simple Harmonic Motion Study Guide
What is Simple Harmonic Motion?
We see oscillatory and periodic motion all around us. A swing in the park moves to and fro; the hands of a clock go around every day; the strings on a guitar vibrate to produce sounds. Yet, all of these motions share commonalities and differences.

In physics, the study of oscillatory motion is important everywhere, from the orbits of planets to the vibration of atoms and molecules. One such oscillatory motion which has a lot of practical uses is the simple harmonic motion (SHM). What makes SHM different from other types of oscillatory motion? Let’s find out!
OSCILLATORY AND PERIODIC MOTION
Before getting to SHM, it is important to understand oscillatory and periodic motion.
Oscillatory Motion
- An oscillatory motion is the to and from motion executed by an object about a mean point.
- A simple example is the motion of a pendulum about its mean position.
- A weight hanging at the end of a long thread moves to and fro until it comes to a stop at the mean or ‘equilibrium’ position.
- At the mean position, the pendulum has maximum velocity, and at the extreme position, a restoring force pulls it back.
Periodic Motion
- A periodic motion is a type of motion that repeats itself over a period of time.
- The movement of the hands of a clock exhibits periodic motion.
- From the example, we can see that not all periodic motion is oscillatory.
- However, the motion of a pendulum is both oscillatory and periodic.
SIMPLE HARMONIC MOTION
- An oscillatory motion becomes simple harmonic when the acceleration of the particle is directly proportional to its displacement from the mean position.
- From this, we can see that all SHM are oscillatory in nature, but not all oscillatory motion is simple harmonic.
- In fact, SHM can be called a special case of oscillatory motion.
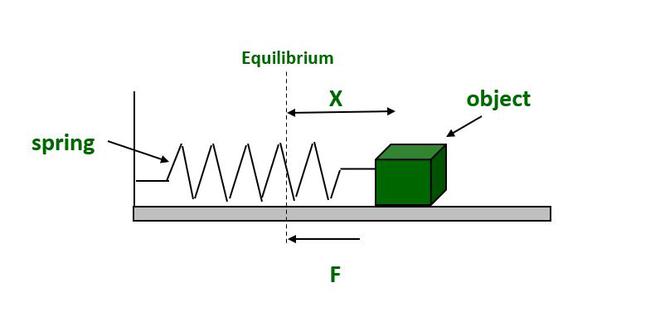
- A simple example of an SHM is the spring-mass system shown in the diagram above.
- When the mass which rests on a frictionless surface is extended, the spring exerts a restoring force equal to the magnitude of the extension.
- The force generated by the spring is given by the formula:
F = -kx
K is the spring constant measured in N/m
X is the displacement of the mean position
The negative sign indicates that the force acts in the opposite direction of motion
Difference Between Simple Harmonic, Periodic and Oscillation Motion
Periodic Movement
• After an equal amount of time has passed, a motion repeats itself. Consider a smooth circular motion.• There is no place of balance.• No restorative force exists.• There is no steady state of balance.
Oscillation Motion
• A particle moving back and forth around a mean position is referred to as oscillatory motion when It travels on either side of the equilibrium or mean position.• It is a particular kind of periodic motion that is limited by two extremes. Simple pendulum oscillation and the spring-mass system are two examples.• The mean position (or equilibrium position) along any route is the location at which an item will continue to move while oscillating between two extreme positions around a fixed point. The route itself is not a restriction.• A reliable equilibrium position is the mean position.
SHM, or Simple Harmonic Motion
• It is a particular instance of oscillation along a straight line between the two extreme locations (the path of SHM is a constraint).• The route of the item must be a straight line.• A restoring force will aim towards the equilibrium position (or average position).• Simple harmonic motion has a stable equilibrium at the mean position.
Simple Harmonic Motion Types
Simple Harmonic Motion, or SHM, may be divided into two categories:
• Linear SHM• Angular SHM
Simple Harmonic Linear Motion
Simple harmonic motion is referred to when a particle oscillates in a straight line and around a set point (known as the equilibrium position).Consider a spring-mass system.
Conditions for Linear SHMThe restoring force or acceleration imposed on the particle should always be inversely proportional to the particle’s displacement and pointed in the direction of the equilibrium position.
__ Angular Simple Harmonic Motion__
An angular simple harmonic motion occurs when a system oscillates angularly long with respect to a fixed axis.
Conditions to Execute Angular SHM
The restoring torque (or) angular acceleration exerted on the particle should always be proportionate to the particle’s angular displacement and pointed in the direction of the equilibrium location.
Simple Harmonic Motion Key Terms
Mean Position
The location where there is no net force acting on the particle.
SHM amplitude
It is the particle’s greatest deviation from the mean position.
Time Period and SHM Frequency
The time period is the least amount of time required to complete one oscillation, or it can alternatively be described as the minimum amount of time after which the particle continues to repeat its motion.T = 2π/ω
Frequency is defined as the quantity of oscillations per second.
Angular frequency = 2πf = 2π/T and frequency = 1/T
Phase in SHM
The condition of a vibrating (or oscillating) particle with respect to its displacement and vibration direction at any given moment is known as the particle’s phase.
SIMPLE HARMONIC MOTION EXAMPLES
- A simple pendulum
- Vibrating springs
- The motion of a torsion pendulum
- The vibration of atoms inside the atomic lattice
- Liquid oscillating in a U-tube
- Rolling a marble over a concave surface
SUMMARY
- An oscillatory motion is the to and from motion executed by an object about a mean point.
- A periodic motion is a type of motion that repeats itself over a regular time interval.
- In a simple harmonic motion, the acceleration of the particle is directly proportional to its displacement from the mean position.
FAQs
Q. What is unique about simple harmonic motion?
An SHM is a special type of oscillatory motion that is also periodic. The restoring force in an SHM is directly proportional to the displacement of the object from the mean position.
Q. What change can be made to increase the period of the oscillation if spring is attached to a mass and oscillates freely in simple harmonic motion?
Considering the characteristics of simple harmonic motion, to increase the period of oscillation, the spring stiffness needs to be reduced, and the mass needs to be increased.
Q. What is the importance of simple harmonic motion?
Simple harmonic motion finds application in all fields, starting from the design of circuits to the study of gravitational waves.
Q. What is the maximum displacement of a body in simple harmonic motion?
The maximum displacement of a body in SHM is called its amplitude.
We hope you enjoyed studying this lesson and learned something cool about Simple Harmonic Motion! Join our Discord community to get any questions you may have answered and to engage with other students just like you! We promise, it makes studying much more fun!😎
]]>