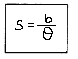CBSE Class 11 Physics Chapter 2 Revision Notes

Chapter 2: Units and Measurement Revision Notes

• Measurement: The measurement process is essentially a comparison process. To determine how many times a standard amount of a physical quantity is present in the quantity being measured, we must first determine how many times a standard amount of that physical quantity is present in the quantity being measured.

• The magnitude of the number obtained is called the unit of the physical quantity, and the standard used is called the unit of the physical quantity.

• Unit: A physical quantity’s unit is an arbitrarily chosen standard that is widely accepted by society and can be used to measure other physical quantities of similar nature.

• Standard: A standard of a physical quantity is the actual physical embodiment of that physical quantity’s unit.

• We need the numerical value (n) and the unit (μ) to express any measurement.

  Physical quantity measurement = Numerical value x Unit = n x μ

• Consider the following scenario: A rod’s length is 5 m, here 5 is the numerical value and m (metre) is the length unit.

Fundamental Physical Quantity/Units

• It is a quantity that can be expressed without the use of any other physical quantity. It can’t be resolved any further in terms of another physical quantity. It’s also known as the fundamental physical quantity.
• Fundamental units are the units of fundamental physical quantities.
• For example, in the M. K. S. system, mass, length, and time are all expressed in kilograms, meters, and seconds, respectively. These are fundamental units.

Derived Physical Quantity/Units

• The term derived physical quantities refers to all physical quantities that can be derived from the combination of two or more fundamental quantities or expressed in terms of basic physical quantities.
• All other physical quantities units, which can be derived from fundamental units, are referred to as derived units. Units of velocity, density, and force, for example, are m/s, kg/m3, and kg m/s2, respectively, and are examples of derived units.

Systems of Units

• Previously, different countries used three different unit systems. CGS, FPS, and MKS were the systems in question.
• Internationally, the SI system of units is now used. Seven quantities are used as the base quantities in the SI unit system.

(i) CGS System: The units of length, mass, and time are the centimeter, gram, and second, respectively.

(ii) FPS (First Person Shooter) System: The units of length, mass, and time are the foot, pound, and second, respectively.

(iii) MKS System: The length is measured in meters, the mass is measured in kilograms, and the time is measured in seconds. The units of length, mass, and time are the meter, kilogram, and second, respectively.

(iv) The International System of Units (SI): The units of measurement for length, mass, time, electric current, thermodynamic temperature, amount of substance, and luminous intensity are meter, kilogram, second, ampere, kelvin, mole, and candela.

Fundamental Units Definitions

Source

Supplementary Units

• There are two additional base units in addition to the seven mentioned above.
• The terms for angle and solid angle are (i) radian (rad) and (ii) steradian (sr).

Source

Advantages of the SI Unit System

• It is an internationally recognized unit system
• It is a rational unit system
• It is a coherent unit system
• It is a metric system
• It is closely related to the CGS and MKS systems of units
• It uses the decimal system, making it more user-friendly.

Other Important Length Units

• Larger units of length, such as the ‘astronomical unit,’ ‘light year,’ and parsec,’ are used to measure large distances, such as the distances between planets and stars.
• One astronomical unit is the average distance between the Earth and the sun.

1 AU is equal to 1.496 x 10¹¹ m.

• A light year is the distance traveled by light in vacuum in one year.

9.46 x 10¹⁵ m is the length of a light year.

• A parsec is the distance between two points where an arc of length one astronomical unit subtends an angle of one second.

3.08 x 10¹⁶ m = 1 parsec

• 1 fermi = If = 10^-15 m • Size of a tiny nucleus = 1 fermi
• 1 angstrom = 1A = 10^-10 m is the size of a tiny atom.

Parallax Method

• This method is used to calculate the distance between planets and stars.
• Parallax: Close your right eye and then your left eye to look at a pen held in front of your eyes. What are your observations? The pen’s position changes in relation to the background. The term parallax refers to the relative shift in the position of the pen (object) in relation to the background.
• If a distant object, such as a planet or star, subtends parallax angle 0 on an arc of radius b (known as basis) on Earth, then its distance from the basis is given by units.

Source

• We can use an electron microscope and tunneling microscopy to estimate the size of atoms. We can estimate the size of nuclei of different elements using Rutherford’s a-particle scattering experiment.
• Time is commonly measured with pendulum clocks, mechanical watches (which use the vibrations of a balance wheel), and quartz watches. Cesium atomic clocks have a precision of 1 part in 10¹³ and can be used to measure time (or to a maximum discrepancy of 3 ps in a year).
• The kilogram is the SI unit of mass. When dealing with atoms, molecules, and subatomic particles, the “unified atomic mass unit” (1 u) is used, with 1 u equaling 1.66 x 10^-27 kg.

Source

Dimensions

• The powers to which the fundamental units of mass, length, and time must be raised to represent the given physical quantity are known as the dimensions of a physical quantity.

Formula for Dimensions

• A physical quantity’s dimensional formula is an expression that tells us how and which of the fundamental quantities go into the unit of that quantity.
• The fundamental quantities, such as length (L), mass (AT), time (T), electric current (I), temperature (K), and luminous intensity (L), are usually written with a capital letter (C).
• To get the dimensional formula of any given physical quantity, we write appropriate powers of these capital letters within square brackets.

Dimensional Applications

• Dimensional formulae and the concept of dimensions are used in the following ways:

(i) Verifying the obtained results

(ii) Conversion of units from one system to another

(iii) Trying to figure out how physical quantities relate to each other

(iv) Model scaling and analysis.

• The principle of homogeneity of dimensions is the underlying principle for these applications.
• The ‘net’ dimensions of the various physical quantities on both sides of a permissible physical relation must be the same, and only dimensionally similar quantities can be added to or subtracted from each other, according to this principle.

Limitations of Dimensional Analysis

The dimensions method has the following drawbacks:

(i) The value of a dimensionless constant cannot be calculated using this method.

(ii) Equations containing trigonometric, exponential, and logarithmic terms cannot be analyzed using this method.

(iii) If a physical quantity in mechanics is dependent on more than three factors, a relationship between them cannot be established because equalizing the powers of M, L, and T yields only three equations.

(iv) it does not distinguish between vector and scalar quantities.

Significant Figures

• The significant figures are a measure of the precision with which a physical quantity is measured.
• In a measurement, significant figures are the digits in a physical quantity that are known with certainty, plus the first digit, which is uncertain.

The Number of Significant Figures Calculation Rules

(i) Every non-zero digit is important.

(ii) Between non-zero digits, all zeros are significant.

(iii) In numbers without a decimal point, all zeros to the right of the last non-zero digit are meaningless.

(iv) All zeros to the right of the decimal point and to the left of a non-zero digit are meaningless.

(v) To the right of a decimal point, as well as to the right of a non-zero digit, all zeroes are significant.

(vi) In addition and subtraction, the least decimal place among the values operated should be retained in the result.

(vii) When multiplying and dividing, we should use the smallest number of significant figures that corresponds to the least precise number in the operation.

(viii) If scientific notation is not used:

(a) The trailing zeroes are not significant for a number greater than 1 without a decimal.

(b) The trailing zeros in a decimal number are significant.

Error

• The physical quantity’s measured value is frequently different from its true value. Every measurement made with any measuring instrument yields an approximate number with some uncertainty. Error is the term for this uncertainty. There is an error in every calculated quantity that is based on measured values.

Causes of Errors

The following are some of the reasons for measurement errors:

Source

• Least Count Error is a type of error that occurs when a number is counted The least count error is the error related to the instrument’s resolution. It’s possible that the least count isn’t small enough. The least count equals the maximum possible error.
• Instrumental Error is a term that refers to a mistake that is made This is due to a problem with the calibration or a change in the environment (e.g., thermal expansion of a measuring scale). A zero error can also occur in an instrument. It is necessary to make a correction.
• Random Error: This is also referred to as a chance error. It causes the same measurements to yield different results when taken multiple times. The Gaussian law of normal distribution is assumed to apply to these errors.
• Unintentional Error: This error produces results that are either too high or too low. Calculations do not include measurements involving this error.
• Systematic Errors: Systematic errors are those that have a tendency to go in one direction, either positive or negative. Systematic errors include weighing errors caused by air buoyancy and calorimetry errors caused by radiation loss. Manipulation can be used to get rid of them.
• Instrumental error, imperfections in experimental technique or procedure, personal errors are some of the sources of systematic errors.

]]>