Pascal’s Law Study Guide
According to Pascal’s law “A confined liquid’s external static pressure is dispersed or transmitted uniformly throughout the liquid in all directions.
Any surface in touch with a fluid is subjected to static pressure, which acts at right angles to it. Pascal also discovered that the pressure at a given place in a static fluid is the same in all planes traveling through that point. Pascal’s law is also known as Pascal’s principle or the principle of fluid-pressure transmission. Pascal’s law was first formulated in 1653 by French mathematician Blaise Pascal.
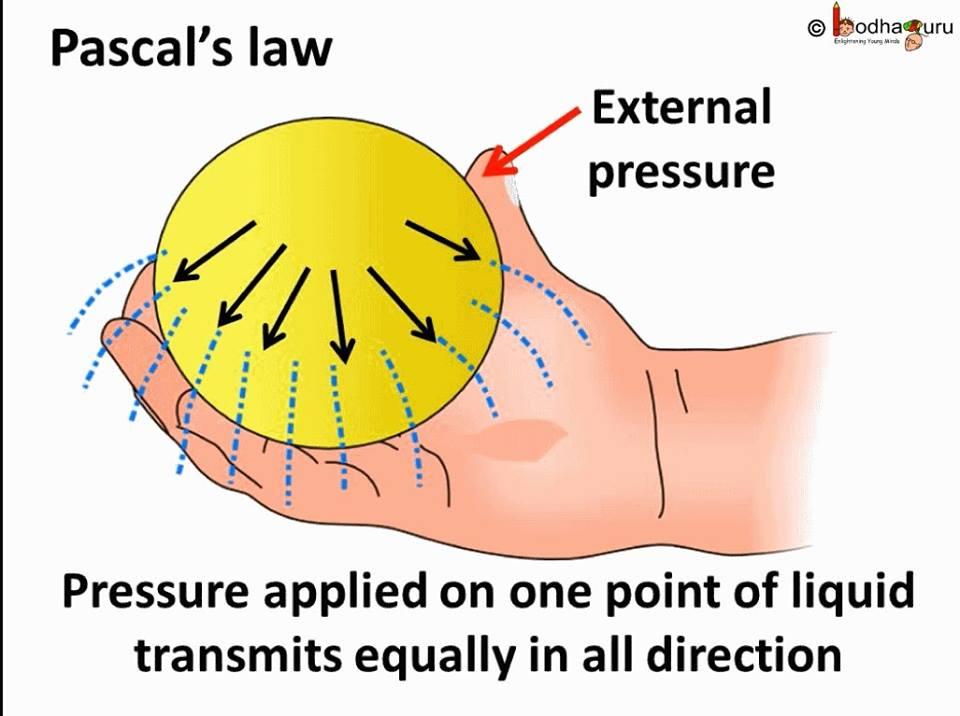
What is Pascal’s Law?
Pascal’s premise can be summed up as follows:
- At rest, pressure changes in any part of fluid are unequally transmitted to all of its locations.
- An enclosed container produces pressure that is applied uniformly and unequally across its surface, acting at right angles to the container’s walls.
- According to another definition, any pressure exerted on any part of the enclosed liquid will be equally transferred throughout it.
Pascal Law Formula
The Pascal law formula is as follows:
PA = F
Where,
- The applied force is F,
- the transmitted pressure is P, and
- the cross-sectional area is A.
Applications of Pascal’s Law
- Hydraulic Lift: The illustration at the top of this page depicts a hydraulic lift in a basic line diagram. The functioning principle of a hydraulic lift is as follows. The idea of equal pressure transmission throughout a fluid (Pascal’s Law) governs its operation.
- A narrow cylinder (in this example A) is connected to a larger cylinder (in this case B) (in this case B). On both ends, airtight pistons are installed. The insides of the cylinders are filled with a non-compressible fluid.
- Pressure applied to piston A is equally transmitted to piston B, allowing the fluid that cannot be compressed to be used. As a result, piston B can be used to raise huge things such as large machinery or automobiles.
- A hydraulic jack and hydraulic press are two further examples, and most cars employ forced amplification in their braking systems
- The hydraulic crane, hydraulic lift, hydraulic jack, and hydraulic brake system are all examples of Pascal’s main applications.
- Pascal’s concept is applied by an excavator digging a hole, a car being lifted by a hydraulic lift, and even squeezing a toothpaste tube.
Hydraulic Brakes
- Hydraulic brakes are generally used in automobiles having large mass like cars, trucks etc. when a heavy vehicle is moving with a high speed a large amount of force is required to stop it within a required distance. Such large retarding force cannot be obtained by simple lever brakes so hydraulic brakes are used.
- Hydraulic brakes work on the principles of Pascal’s law or transmission of fluid pressure. It consist of a massive cylinder and a break cylinder which is connected with a thick metallic pipe filled with a thick oil generally called as breaking fluid. The two cylinders are provided with air tight pistons, the break cylinders are located at the wheels of the vehicles.
- When the breaks are applied it is applied on the massive cylinder with the help of levers between the pedal and the cylinder. The piston then moves forward applying pressure in the break oil. This increases the pressure it is then transmitted to the oil and the pistons of break cylinder are pushed outwards thereby pushing the shoes of the breaks against the rim of the wheel and thus vehicle stops.
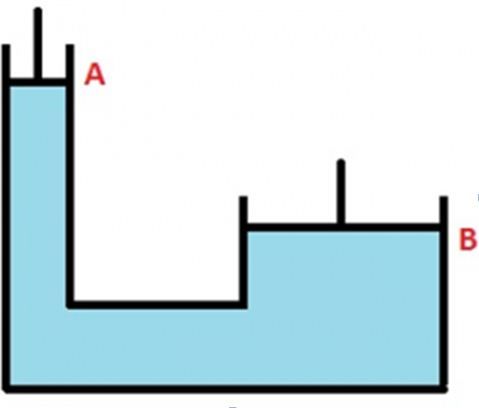
Variation of Pressure with Depth
Every scuba diver knows that the pressure increases with depth below air. Every mountaineer knows that the pressure decreases with the altitude as one climbs into the atmosphere.
Let us take an example of a cylinder which is placed into the tank of water. The bottom of the cylinder must be at a higher pressure than the pressure at the top of the block because it must support the weight of the water in between the top and bottom. The pressure increases with increasing depth
P = P0 + ρghWhere P = Pressure at depthP0 = External pressure ρgh = Rho g and h which is hydrostatic pressure
Example
The hydraulic crane, hydraulic lift, hydraulic jack, and hydraulic brake system are all examples of Pascal’s main applications. Pascal’s concept is applied by an excavator digging a hole, a car being lifted by a hydraulic lift, and even squeezing a toothpaste tube.
Examples of Pascal’s Law
Q.1. A hydraulic press has two cylinders of areas 200cm2 and 1000cm2. If a force of 10N is applied at the plunger, what force is created at the load end?
__Solution: __
Plunger side area, A1 = 200 cm²Load side area, A2 = 1000 cm²Input force, F1 = 10NF2/F1 = A2/A1F2 = A2/A1×F1F2 = 1000/200×10 = 50NForce is multiplied five times when the output side area is five times the input side cylinder.
Q.2. A hydraulic press has cylinder areas in the ratio of 20:1. If the output side piston must move by 20cm, what distance must the input side piston be pushed?
Solution:
F2/F1 = 20/1F2/F1 = d1/d2Given, d2 = 20cmd1 = F2/F1×d2d1 = 20/1×20 = 400cm
The input side piston must be pushed 400cm to make the output side piston move up by 20cm.
Derivation of Pascal’s Law
Consider a right-angled triangle in a dense liquid (rho). Because of the element’s small size, each point is assumed to be at the same depth as the liquid surface. At all of these locations, gravity has the same effect.
The cross-sectional areas of the ABFE, ABDC, and CDFE faces, respectively, should be represented by the letters ab, bd, and cd.Assume that P1, P2, and P3 are, respectively, the pressures conveyed on faces ABFE, ABDC, and CDFE.
A force parallel to the surface is applied by the pressure. The surfaces ABFE, ABDC, and CDFE may each have a force of F1 applied by P1, F2 applied by P2, and F3 applied by P3.
Therefore, Force F1, F2, and F3 is given as:F1 = P1 × area of ABFE = P1 adF2 = P2 × area of ABDC = P2 bdF3 = P3 × area of CDFE = P3 cd
Also, Sin θ = b/aCos θ = c/a
The net force on the prism will be zero since the prism is in equilibrium.
F1 sin θ = F2F1 cos θ = F3P1 ad b/a = P2 bd (eq 1)P1 ad c/a = P3 cd (eq 2)
From 1 and 2P1 = P2 and P1 = P3∴ P1= P2= P3
Summary
- Any surface in touch with the fluid is subjected to static pressure, which acts at right angles to it.
- Pascal also discovered that the pressure at a given place in a static fluid is the same in all planes traveling through that point.
- Pascal’s law is also known as Pascal’s principle or the principle of fluid-pressure transmission. Pascal’s law was first formulated in 1653 by French mathematician Blaise Pascal.
FAQ’s
Q. What is Pascal’s law?
“The external static pressure applied to a confined liquid is dispersed or transmitted evenly throughout the liquid in all directions,” according to Pascal’s law.
Q. What is the application of Pascal’s law?
The principle of Pascal’s law governs hydraulic lifts.
Q. Does Pascal’s law apply to gases?
Pascal’s law holds true for gases. Pascal’s concept is also known as the principle of fluid (water or gas) pressure transmission.
Q. Who stated Pascal’s law?
In 1653, French mathematician Blaise Pascal proposed the Pascal law.
Q. What is the principle of Pascal’s law?
According to Pascal’s law, pressure applied to a confined fluid is transmitted without change in magnitude to all points of the fluid and the container’s walls. Any point in the fluid has the same pressure in all directions.
We hope you enjoyed studying this lesson and learned something cool about Pascal’s Law! Join our Discord community to get any questions you may have answered and to engage with other students just like you! We promise, it makes studying much more fun!😎
]]>